目次
スポンサーリンク
マグフォーマーとは?
マグフォーマーは、ボーネルンド社から2005年に発売が開始されてから15年。あっという間に世界に広がったため、幼児教育に熱心な方はみなさんご存知の知育玩具だと思います。
三角形、四角形、五角形など、さまざまなピースの辺と辺を合わせて立体形に組み立てていくことで、楽しく図形感覚を養うことができます。
辺同士で磁石で繋がる時に「カチッ」という小気味の良い音がしますが、頂点と頂点を細かく合わせるような作業が不要なため、幼児でも比較的簡単に立体図形を作ることができます。
赤ちゃんが飲み込まない大きさ、かつ角が滑らかなため安全性も高く、低年齢の頃から遊べます。
弱点は、価格が高いということだけでしょうか。1ピース200円以上はするので、類似製品の購入を検討する方も多くいらっしゃいますね。
類似品のことは分からないので、あくまでもマグフォーマーの使い方についての記事を書きたいと思います。
マグフォーマーの五角形/六角形のバラ売りを購入しての所感
マグフォーマーは、今までも「知育玩具としては優秀だろうな」と思いつつ、やはりその値段の高さから手が出ませんでした。
ただ、今は単なる「磁石おもちゃ」ですが、小学生高学年以降も眺めたりするには非常に良いので、長い目で考えると「買い」だと思いました。
出費は少しイタいですが、タイミングを見て少しずつ買い足していくと思います。
五角形の12ピースセットを購入
マグフォーマーの導入を検討する際は、ベーシックセットやクリエイティブセットの購入から考える方も多いと思いますが、我が家ではまず五角形と六角形から揃えました。
通常は、正三角形や正方形の組み合わせから揃えると思うのですが、娘はすでに立方体についての理解はある程度しているように思ったのと、保育園にもマグフォーマーがあり、正三角形や正方形の組み合わせには慣れ親しんでいるようなので、我が家ではいきなりの五角形からのマグフォーマー導入をしてみました。
あと、本音をいえば、サッカーボールをマグフォーマーで作ってみたかったというのがありました。
伝統的なサッカーボールの形状は、正五角形と正六角形でつくられていますが、なかなかそれを再現するのは難しい。

それを、マグフォーマーで再現したくなったという、完全に親の趣味ですが、結果的に娘の立体図形の理解の深まりに役立てればよいかな、、と。
マグフォーマーでのサッカーボール作りについては、別途記載する予定ですが、まずはその前に五角形だけで作れる正十二面体を紹介したいと思います。
スポンサーリンク
五角形での正十二面体の作り方
正十二面体は、正多面体の1つで、12枚の正五角形で囲まれた形です。
非常に美しい立体図形の一つですが、折り紙などで簡単に作ることはできません。しかし、マグフォーマーを使うと、幼児でも5分以内に作れます。

マグフォーマーでは、ちょうど正五角形が12ピースで販売されており、こちらを手に入れるだけで正一二面体を作ることができます。税込3,960円ということで、やはり正規品はちょいとお高め😓
↓ 五角形単品
まずは、正五角形を6枚ずつ並べます。

この形を見るだけで、アナ雪大好きムスメは「雪の結晶みたいだね」と大喜び。
遠い受験のことを考えるなら展開図を想像しやすくなりますね。

このようにお皿と帽子を作り、、

2つのパーツを組み合わせて、あっという間に正十二面体の完成です。
正十二面体の簡単な特徴
4歳の娘には、まだ頂点や辺の数などを教えたりはしませんが、備忘録的に簡単な特徴をまとめておこうと思います。
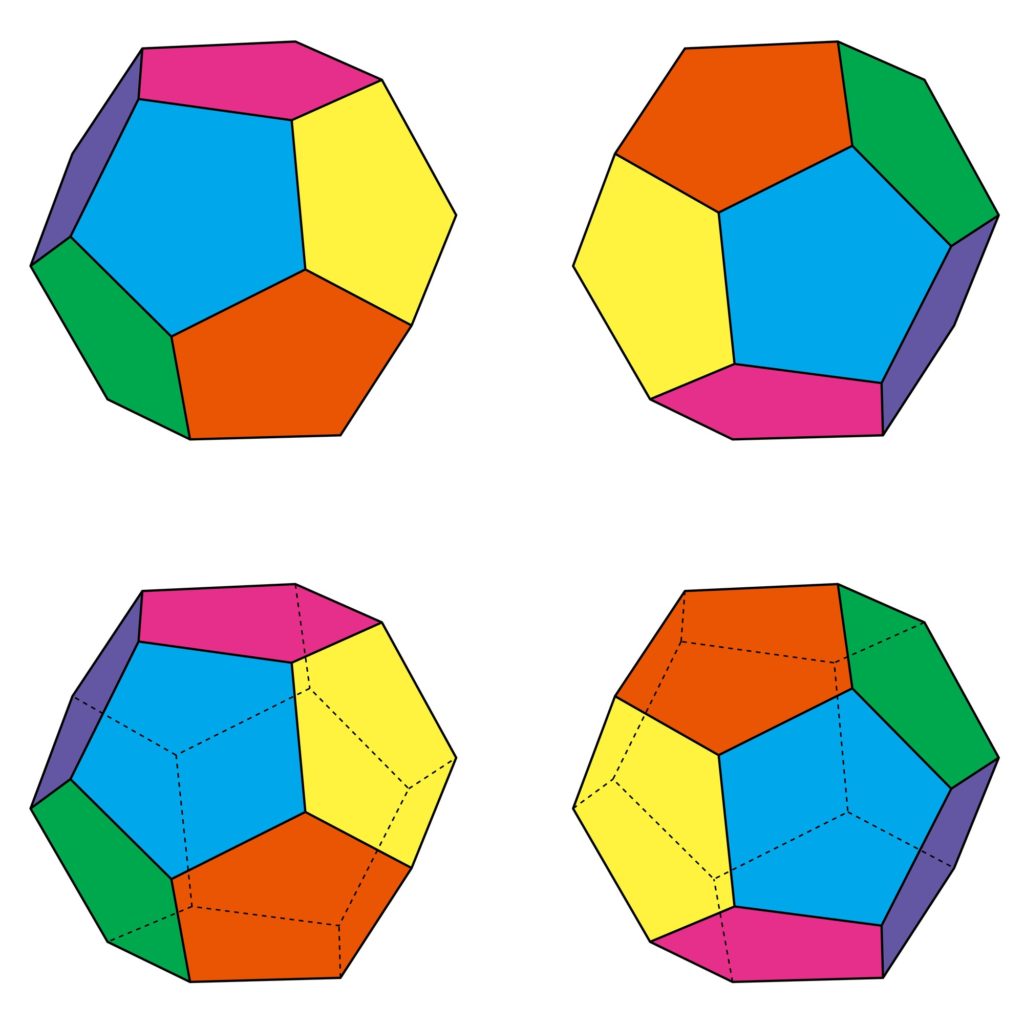
正五角形の数→12個
頂点の数→20個
辺の数→30本
頂点や辺の数などは、丸暗記をするのではなく、小学生以降に自らの力で求められるようになって欲しいですが、まずは幼児の今の段階では「遊びの中で、綺麗な立体を好きになってくれる」と嬉しいですね。
スポンサーリンク
マグフォーマーの六角形と素朴な質問
正多面体は、「正四面体、正六面体、正八面体、正十二面体、正二十面体」の5つしかありません。これらの構造を幼児でも遊びの中で簡単に触れるのに、マグフォーマーは最適です。
将来の受験に生きるというだけではなく、「面がすべて合同な正多角形でできている」というものを、こどもなりに”美しい“と感じ取ってもらえると嬉しいな、と思っています。
ムスメも、マグフォーマーはお気に入りのようで、正十二面体は2-3分で作れるようになりました。
ということで、次の仕掛けのために、今度は正六角形のマグフォーマーを購入することにしました。
こちらは、12枚入りで4,620円。安くはないですが、ムスメが小学生になっても使えると信じ、正五角形に続いて購入してしまいました。しかも2セット!!
繰り返しになりますが、マグフォーマーの六角形は、五角形と同じようにバラで12ピースで販売されています。

↓六角形単品
六角形はムスメにとってはミツバチの巣の形として良く覚えています。

ムスメ自身も、蜂の巣を描く中で、まだ上手には描ききれていないですけれど、六角形だという理解はしている段階です。

正六角形の1つの内角は120度のため、1つの頂点に3枚集まると角度の和が360度となるため、角が平らになり正多面体を作ることはできません。

今はとにかく体験を通じて種を蒔く時期。
「六角形は、なんで形(立体)にできないの?」
という質問をされましたが、さすがにまだ細かくは説明できません。でも、そういう疑問を持つことは、とても良いことですよね👍
六角形と五角形の組み合わせで切頂二十面体を作成
六角形のみだと立体の図形は作れませんが、五角形を混ぜるととても素敵な半正多面体を作ることができます。
そう。サッカーボールの構造として良く知られている、切頂二十面体です。

基本的に、正五角形は全て六角形に囲まれています。

そのルール通りに五角形と六角形を組み合わせていくと、あっという間に組み上がっていきます。

マグネットでの接着がしっかりしているので、組み立ても簡単です。

このようにサッカーボール型である切頂二十面体が完成!
切頂二十面体は、正五角形が12枚、正六角形が20枚の32枚の面で構成されています。
頂点の数は60、辺の数は90と、少し数も大きくなっているため、これらの求め方は小学生になってから教えてみようかなと思っています。
スポンサーリンク
のちの化学への応用!?
ちなみに、幼児・小学生レベルであれば「サッカーボール型」で良いのですが、この形って高校生の化学でも出てきます。
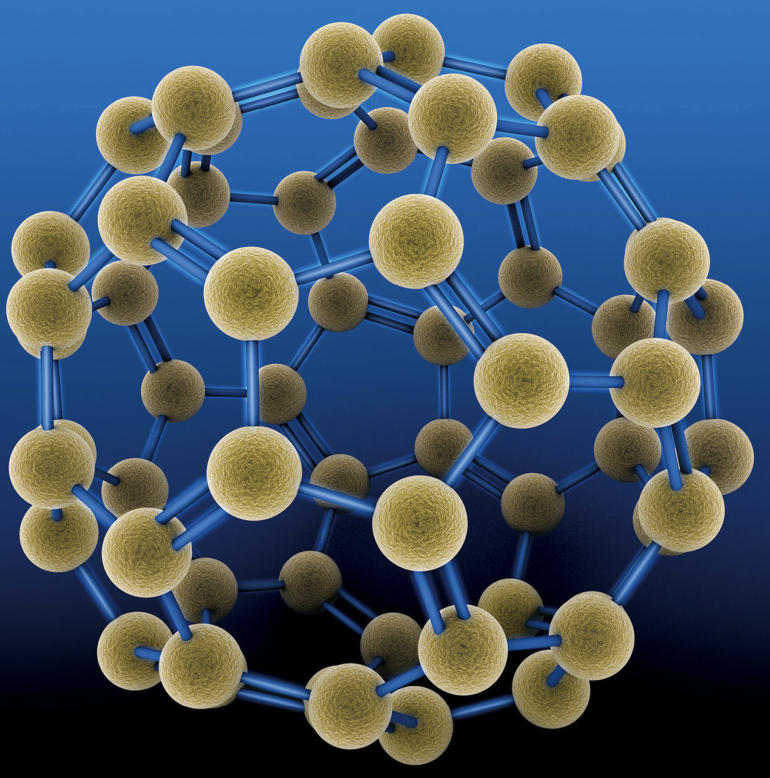
炭素原子60個からなるフラーレンC60というかご状の分子です。この分子構造を発見した科学者は、ノーベル賞も受賞しています。
マグフォーマーでの遊びが、算数や数学の図形感の育成だけではなく、化学を学ぶ際にもアレルギー感なく(むしろ、懐かしさとともに)学んでいけるかもしれませんね。
マグフォーマーの購入方針
マグフォーマーは、普通は複数の形が組み合わさったセットである、ベーシックセットなどから購入されるケースがほとんどだと思っています。
もちろん、ベーシックセットを購入してどんどん自由に作らせていくところからマグフォーマーに親しむのもありだと思うのですが、如何せん安い買い物ではありません😓
それなら、多少なりとも教育効果を高めたいな、と思っていて、そこで思いついたのが、「バラ売りから揃えていく」という揃え方でした。
ぜひ、参考にしていただければと思います!
↓ 五角形単品
↓六角形単品
↓セット買い
















今回は、ムスメが大好きなマグフォーマーについて、様々な形とその活用方法について纏めてみました。
各図形数枚ずつ入ったセット商品が売られていて、それを購入したり検討されている方が多いと思います。
しかし、セット商品に入っていなかったり、入っていても数枚しか入っていない五角形・六角形を使って、更に立体感覚を養ったり、ひいては将来の中学受験、大学受験の基礎となるような使い方を具体的に紹介します。